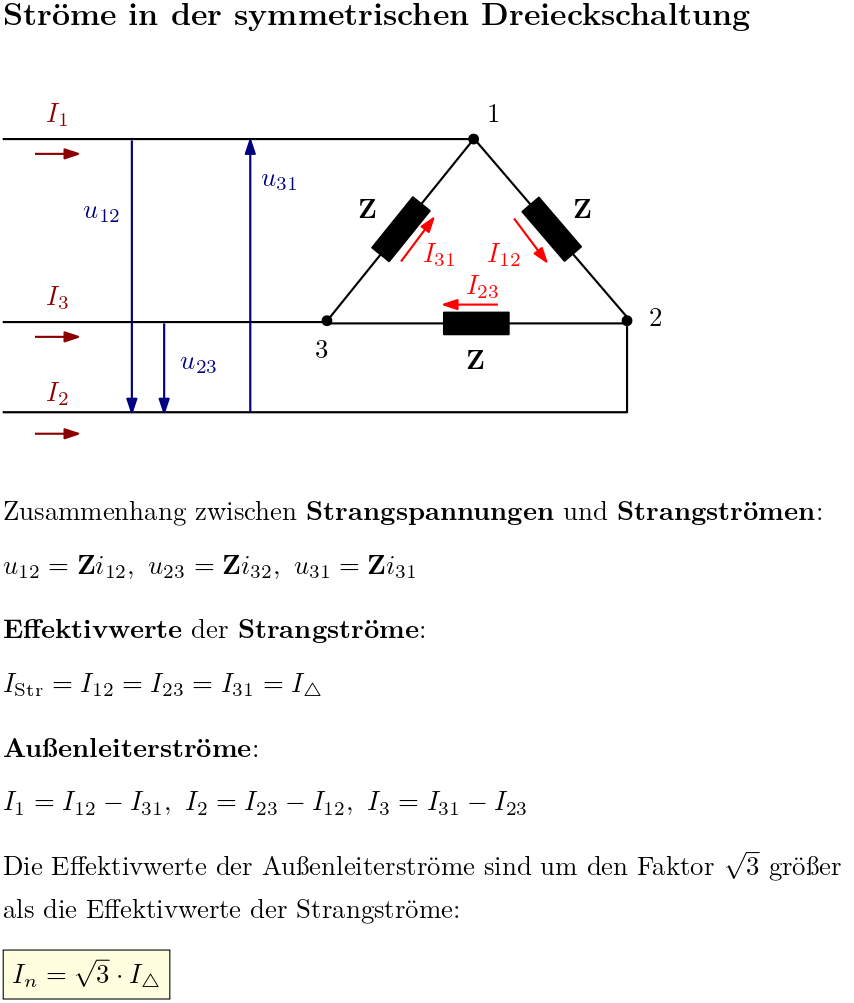
Eine tiefgehende Analyse der symmetrischen Dreieckschaltung im Drehstromsystem steht im Fokus dieses Artikels. Es werden die Struktur und die Beziehungen zwischen Außenleiter- und Strangspannung sowie Außenleiter- und Strangstrom erörtert. Zudem wird die Berechnung verschiedener Leistungen, wie Wirk-, Blind- und Scheinleistung, dargestellt.
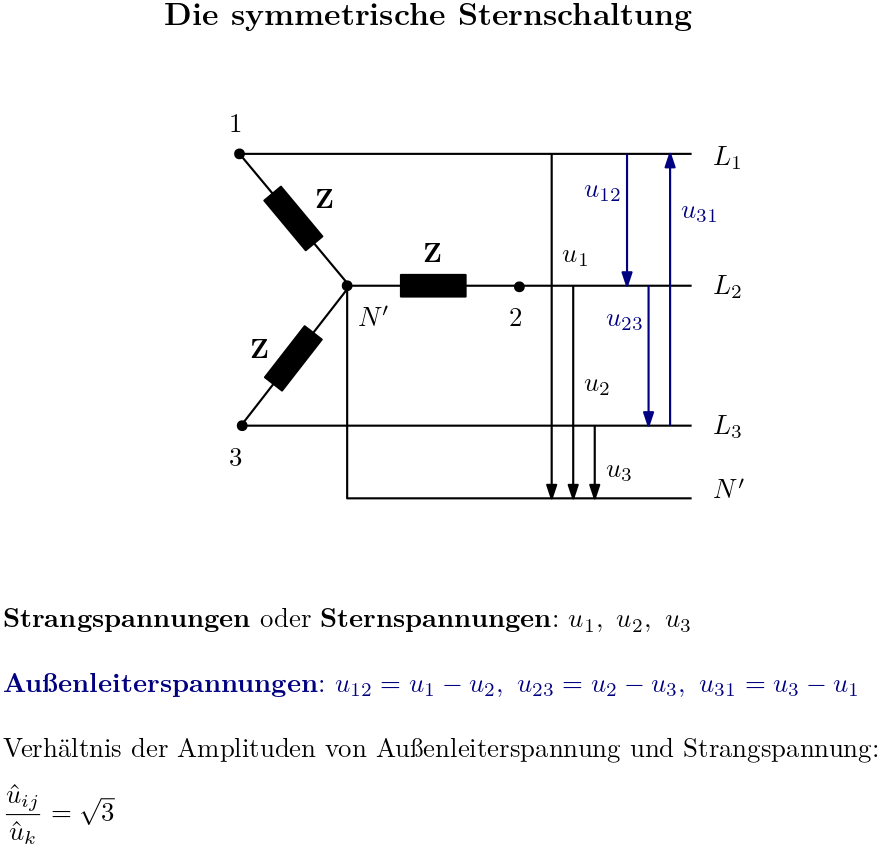
Im Fokus des Artikels steht die Technik der symmetrischen Sternschaltung in Drehstromsystemen. Ausgehend von phasenverschobenen Spannungen, die ein Generator mit verdrehten Wicklungen erzeugt, wird die Verkettung von Spannungsquellen und Verbrauchern aufgezeigt. Ein tiefer Einblick in die Entstehung der Sternschaltung und die relevante Leistungsberechnung rundet den Beitrag ab.
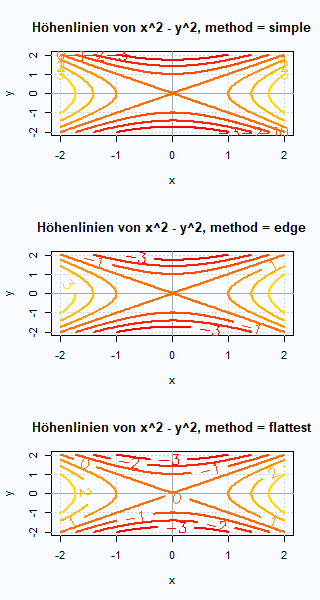
Die Funktion contour() stellt eine effektive Methode zur Darstellung der Höhenlinien einer reellwertigen Funktion auf einem zweidimensionalen Gebiet dar. Oftmals bieten diese eine klarere Darstellung als perspektivische dreidimensionale Graphen, die beispielsweise mit persp() erzeugt werden können. Anhand einfacher Beispiele wird die Nutzung der Eingabewerte von contour() verdeutlicht.
Pünktlich zu Halloween erhebt sich die Frage nach verborgenen Geheimnissen in der digitalen Welt. Insbesondere der Kauf einer Domain kann mehr als nur einen Namen bedeuten: Eine düstere Vergangenheit mit Spam, Blacklistings oder rechtlichen Problemen kann wie ein unsichtbarer Geist die frisch erstellte Website heimsuchen. Dies unterstreicht die Bedeutung einer gründlichen Überprüfung vor dem Domainkauf.
Die elementaren Bausteine der Datenverarbeitung und -speicherung in Java sind primitive Datentypen. Sie gewährleisten eine effiziente Speicherung einfacher Werte ohne den Overhead von Objekten. Dieser Artikel dient als Einführung in die Grundmerkmale der primitiven Datentypen und beleuchtet ihren Speicherbedarf sowie ihre Wertebereiche.
Die Verwaltung des Mono-Projekts wurde unerwartet an WineHQ abgetreten, markiert einen Wendepunkt im .NET-Ökosystem. Dieser bedeutsame Übergang löst Debatten über Monos Vermächtnis und seine künftige Entwicklung aus.
Das ultimative Textabenteuer erwartet Entwickler auf Vim-Racer.com. Hier stellen sie ihre Navigationskünste in Vim auf die Probe und liefern sich einen rasanten Wettkampf gegen Gleichgesinnte. Durch Code fliegen, den Turbo einschalten und der Schnellste auf der Tastatur sein - und das alles ohne Fingerkrämpfe oder Emacs-Verirrungen. Ein Highspeed-Heldenepos im Editor-Rennsport steht bevor.
Der Artikel beleuchtet vier Methoden zur Listenfilterung in Python: Iteration, die filter-Funktion, List Comprehension und die itertools-Bibliothek. Unterschiedliche Stärken und Schwächen machen jede Methode für verschiedene Anwendungsfälle und Szenarien geeignet.
Convolutional Neural Networks (CNNs) zählen zu den essenziellsten und wirkungsvollsten Verfahren in der gegenwärtigen Computer Vision. Sie revolutionieren Bereiche wie Bildklassifizierung, Objekt- und Gesichtserkennung, indem sie Computern das Erkennen spezifischer Objekte in zweidimensionalen Bildern ermöglichen. Der Artikel beleuchtet die Grundkonzepte eines CNNs und illustriert anhand eines simplen Beispiels den Aufbau eines eigenen CNNs.
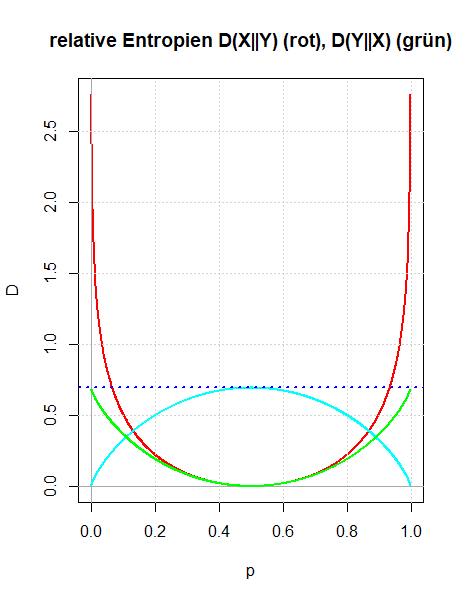
Zwei Ansätze zur Motivation der relativen Entropie werden beleuchtet: Sie wird entweder als Erweiterung der gegenseitigen Information betrachtet oder als Weiterentwicklung von Boltzmanns Überlegungen zur Entropiedefinition, bei der die Annahme gleich wahrscheinlicher Mikrozustände aufgegeben wird. Der Wert der relativen Entropie in der Quantifizierung der Unterschiede zwischen zwei Wahrscheinlichkeitsverteilungen wird durch den zweiten Ansatz klarer.
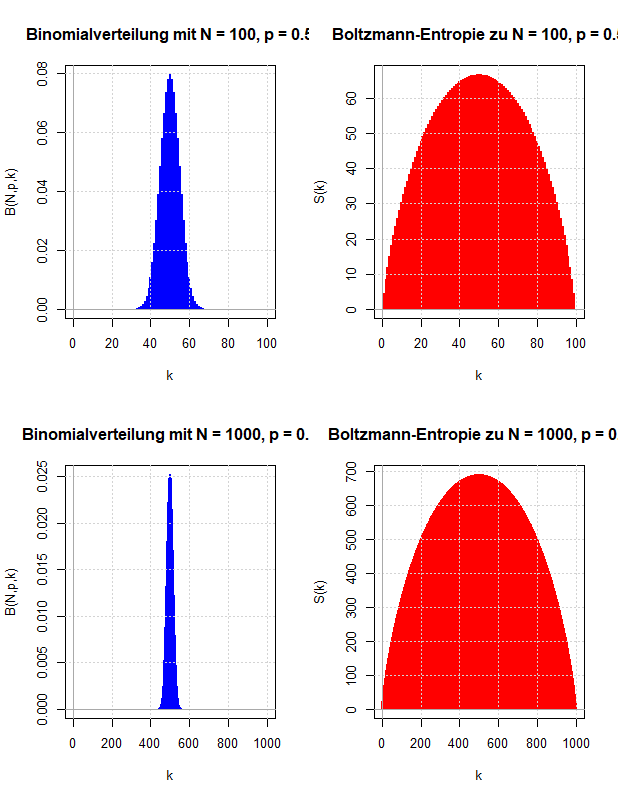
Ludwig Boltzmanns mikroskopische Erklärung für die niemals sinkende thermodynamische Entropie bildet die Basis für die Definition der Entropie in der Wahrscheinlichkeitstheorie. Diese dient zur Quantifizierung der Unsicherheit über den Wert einer Zufallsvariable.
Entropien und gegenseitige Information werden im Kontext von Wartezeitproblemen beim Ziehen ohne Zurücklegen erläutert. Als Zufallsvariablen dienen die Zeitspannen bis zum ersten Treffer sowie vom ersten bis zum zweiten Treffer.
YAML Ain't Markup Language" oder "YAML", eine Datenformatsprache, ist ein wesentliches Werkzeug in zahlreichen Anwendungen, einschließlich CI/CD-Pipelines, Docker, Kubernetes und weiterer Software. Der vorliegende Artikel beleuchtet den Einsatz von SnakeYAML in Verbindung mit Java - einer potenten Bibliothek, die das Einlesen von YAML-Dateien als Map oder direkt als benutzerdefinierte Typen (POJOs) erlaubt.
In der komplexen Welt der Wahrscheinlichkeitsverteilungen zweier Zufallsvariablen finden Begriffe wie gemeinsame und bedingte Entropie Anwendung. Diese sind durch die Kettenregel miteinander verbunden und führen zur Einführung der gegenseitigen Information - eine neue, symmetrische Größe. Sie illustriert die Information, die eine Zufallsvariable über die andere bereithält. Die Definition und Veranschaulichung der gegenseitigen Information erfolgt anhand einfacher Beispiele.
Die bedingte Entropie, ein Maß für die Unsicherheit eines zufälligen Ereignisses, basiert auf bedingten Wahrscheinlichkeiten und lässt entweder ein Ereignis oder eine Zufallsvariable zu. Dieser Artikel beleuchtet die Definition der bedingten Entropie und ihren Zusammenhang mit der gemeinsamen Entropie zweier Zufallsvariablen, illustriert durch einfache Beispiele.
Die Entropie als Maß der Unsicherheit in Wahrscheinlichkeitsverteilungen ist ein zentraler Aspekt der Zufallsexperimente. Bei unabhängigen Experimenten wird erwartet, dass sich die Entropien addieren. Der Artikel führt die gemeinsame Entropie H(X, Y) von zwei Zufallsvariablen ein, um diese Theorie zu präzisieren. Es wird deutlich gemacht, dass die gängige Definition der Entropie tatsächlich die Additivität bei unabhängigen Zufallsvariablen X und Y aufweist.
Dieser Artikel beleuchtet die Eigenschaften freier und gebundener Energie anhand der isochoren Erwärmung. Der Fokus liegt auf der Darstellung von Veränderungen beim Übergang vom US- zum TS-Diagramm, mit besonderem Augenmerk auf der freien Energieformel F = U - TS und der gebundenen Energie G = TS.
Der Artikel beleuchtet die Anwendung der Funktionen substr() und substring() in R, die zur Extraktion von Substrings aus einem String genutzt werden. Dabei wird erläutert, wie durch Angabe von Indizes Substrings lokalisiert und in der replacement-Version modifiziert werden können, während der restliche String unverändert bleibt. Zudem wird die vektorisierte Verarbeitung von Zeichenketten thematisiert.
Docker-Volumes sind ein zentraler Aspekt in Containeranwendungen, da sie eine Plattform für das Speichern, Verwalten und Zugreifen auf Daten sowohl innerhalb als auch zwischen Containern und dem Host-Computer darstellen. Ihre Bedeutung wird hervorgehoben, wenn es darum geht, Daten über den gesamten Lebenszygklus eines Containers hinweg zu erhalten, den Datenaustausch zwischen Containern zu ermöglichen und die Datenintegrität in zustandsbehafteten Anwendungen zu gewährleisten.
Die aktuelle Preisstrukturänderung von Unity, einem führenden Spiele-Engine-Unternehmen, sendet Schockwellen durch die Spieleentwicklungsbranche. Bei betroffenen Game-Studios könnte diese Änderung des Lizenzmodells erhebliche Auswirkungen haben. Die Reaktionen sind durchweg eindeutig.
Dieses Tutorial navigiert durch die Grundlagen von Kubernetes und implementiert eine einfache Spring Boot Anwendung in einem lokalen Kubernetes-Cluster mit K3D. Ein Glossar mit grundlegenden Konzepten rund um Containerisierung und Kubernetes wie Pods, Services und Deployments ist enthalten. Grundkenntnisse in Docker und Java/Maven sind notwendig.
Textverarbeitung mit R: Die Funktion paste() optimiert das Zusammenfügen von Vektoren. Ähnlich der Funktion paste0() verwandelt sie Vektoren in Zeichenketten, fügt Komponenten zusammen und erstellt daraus eine einzige Zeichenkette. Mit optionalen Trennungszeichen in zwei Schritten ist diese Funktion eine erweiterte Alternative zu paste0(). Der Artikel beleuchtet die Anwendungsfälle, Vorteile und Spezialfälle dieser Methode.
Textverarbeitung mit R: Die Funktion paste0() zum Zusammenfügen von Vektoren" beleuchtet die Nutzung der Funktion paste0() in R zur Verknüpfung von Vektorkomponenten, die in Zeichenketten umgewandelt werden. Unterschiedliche Anwendungen, wie die Rückgabe von Zeichenkettenvektoren ohne gesetztes collapse-Argument oder die Zusammenfügung von Komponenten zu einer Zeichenkette mit gesetztem collapse-Argument, werden ausführlich erklärt.
Dieser Artikel beleuchtet die Funktionen von format.info(), formatC() und prettyNum() in der Textverarbeitung mit R. Erklärt werden die Rückgabewerte und Formatierungsanweisungen, die dabei Anwendung finden. Besonders die Nähe von formatC() zur Programmiersprache C sowie die Verwendung von prettyNum() zur Zahlenformatierung stehen im Fokus.
OpenAIs kürzlich publizierte Anleitung zur Konfiguration des GPTBots für Webzugriffe hat eine Diskussion um Nutzung und Eigentumsrechte von Inhalten beim Training von KI-Modellen angestoßen. Die DeviantArt-Community hat bereits zuvor auf diese Frage reagiert und entsprechende noai und noimageai Meta-Tags eingeführt.
Die nächste Generation des Open-Source-Modells für Large Language Models, Llama 2, steht im Fokus einer Kooperation zwischen Microsoft und Meta. Mit verbesserten Leistungsdaten und vielseitigeren Anwendungsmöglichkeiten soll das Modell, das für Forschung und kommerzielle Nutzung kostenfrei ist, seinen Vorgänger übertreffen.
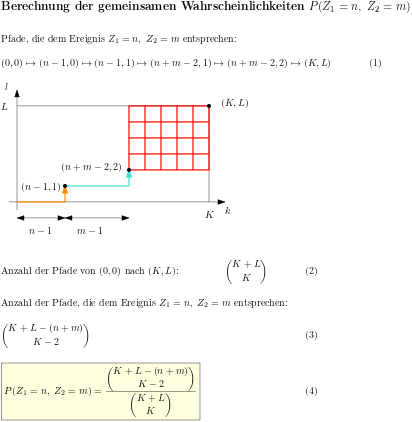
Zufallsexperimente wie das Ziehen mit und ohne Zurücklegen werden in diesem Artikel in eine Zufallsbewegung auf einem Gitter transformiert. Diese Umformulierung ermöglicht eine ansprechendere Veranschaulichung vieler Herleitungen. Insbesondere wird dies für die Verteilungen von Zufallsvariablen demonstriert, welche die Trefferanzahl oder Wartezeit bis zum bestimmten Treffer beschreiben.
Master-Detail-Ansichten, die in GUI-Anwendungen zur hierarchischen Darstellung zusammengehöriger Daten genutzt werden, werden in diesem Artikel durch zwei Implementierungen in Tkinter mit Python präsentiert.
ChatGPT, ein bereits mächtiges Werkzeug, gewinnt durch seine Integration in die Kommandozeile an Effektivität. Der Artikel präsentiert eine detaillierte Anleitung zur Erstellung von drei Skripten, die die ChatGPT API direkt in die zsh Shell einbinden - mit minimalen zusätzlichen Bibliotheken und nur wenigen Codezeilen.
Die Taylor-Polynome sind ein leistungsfähiges Werkzeug zur Approximation von Funktionen. Im Fokus des Artikels steht die Herleitung des Restgliedes in Integraldarstellung, um die Genauigkeit der Approximation zu quantifizieren. Aufgezeigt wird die Berechnung durch sukzessive partielle Integration, vorausgesetzt, die Funktion ist hinreichend oft stetig differenzierbar.